条件化可变形模板 (arXiv 1908.02738)
★★★☆ Learning Conditional Deformable Templates with Convolutional Networks. [arXiv 1908.02738]
- 问题关键词:医疗图像处理,图像配准,对齐 alignment,对应关系 correspondence
- 方法关键词:条件化模板,形变场,极大似然估计,微分同胚变换 diffeomorphism transform
- 模板可以看成是对数据变化模式的概括。
作者信息:
- Adrian Vasile Dalca:研究方向主要是概率模型和医疗图像分析。博士毕业于MIT CSAIL的医疗视觉研究组(Medical Vision Group),导师是Polina Golland。目前在MIT和哈佛医学院做博士后。
- Marianne Rakic:来自ETH D-ITET和MIT CSAIL的研究人员,没有找到个人主页。
- John Guttag:比较老的一个教授,有自己的Wikipedia页面。目前在MIT CSAIL带领数据驱动推断研究组(Data-Driven Inference Group),他曾经担任MIT EECS的主任,是美国科学院(American Academy of Arts and Sciences)院士。主要研究方向是医疗影像处理,但是同时也涉及运动和财经数据分析相关的领域。
- Mert Rory Sabuncu:康奈尔大学的副教授,主要研究生物医学数据分析,尤其关注脑和神经科学。博士毕业于普林斯顿大学,曾跟随Polina Golland在MIT CSAIL做博士后。
这个工作的任务其实是生成一些可变形模板,仅考虑怎么更好地生成,而没有太讨论用这个模板来做什么(实验中好像有简单涉及)。这里所谓的“更好”,主要包括两个方面,一是生成速度快,包括生成模板本身和图像到模板(或者模板到图像)的变换;二是能够以属性为条件来针对性地生成模板,并且学习这种条件化的模板时能够用到数据集中所有的数据,不需要对数据集进行实际划分来分别去学习模板。
方法:做法上其实比较简单,首先以属性\(a_i\)作为输入用一个网络预测模板\(t\),然后以模板\(t\)和图像\(x_i\)作为输入用另一个网络\(g_{v, \theta_v}(t, x_i)\)预测速度场\(v_i\)(velocity field),再根据速度场通过积分(integration layer)计算出对应的形变场\(\phi_{v_i}\)(deformation field),之后通过形变场\(\phi_{v_i}\)将模板\(t\)变换为输入(对输入\(x_i\)进行重构)。
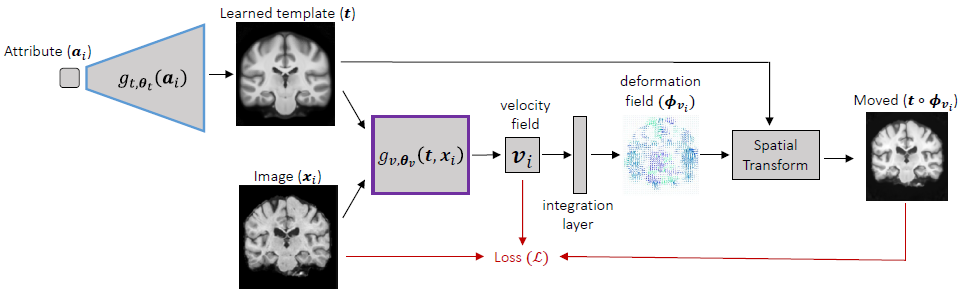
其中对于模板\(t\),如果不采用条件化的生成方式,例如没有属性信息的时候,那可以直接学习\(t\),而不需要学习一个生成\(t\)的模型。
感觉这个方法的关键点主要有两个:采用神经网络作为预测器,采用随机梯度下降进行模型优化。方法中采用了两个神经网络来分别预测模板和速度场(进行图像校准),构建起一个端到端的模型,然后这样就可以采用随机梯度下降法来对整个模型进行优化,这样不管是训练还是测试都会比之前的方法高效。
其实在计算机视觉领域,这样的模型应该算是很普通和常见的了,将现有预测器等替换为神经网络或者用神经网络预测未知量从而构造端到端的基于学习的(learning based)模型是一个基本套路,而条件化的思想在各种生成模型中已经得到了广泛应用。不过这个工作侧重于医学图像的处理(虽然实验大部分是在MNIST数据集上做进行),可能在这个方向上,这个模型还是具有一定的新意并且解决了现有方法的一些问题。
虽然在方法上我感觉不是很新鲜,但是可能只是从最终模型的结构上来看。这个工作实际上是设计了一个生成图像的概率模型,通俗的说这主要体现在损失函数上,即模板变换之后重构图像,如何衡量重构结果和原始输入之间的差异,以及加入的约束。
自己的一点想法:
- 生成模板的时候可以采用残差的方式,平均图像+残差,其中残差通过属性来预测,平均图像作为初始化,其也可以在学习的过程中更新。
- 如果校准的时候不针对每个图像进行优化,而是用一个学好的网络来预测速度场/形变场,这样也许误差会更大?换言之模型的泛化能力对校准质量非常关键。
- 不同属性的图像采用不同的模板,那么相互之间怎么比较形变场呢?似乎只能在同属性的图像之间比较了。不过这样看来不同属性带来的差别也许能方便地看出来,直接比较对应的模板就可以,学出来的可能比平均图像要更有代表性一点。
- 为什么不直接预测形变场和在形变场上加约束,而要先预测速度场再积分得到形变场?可能和微分同胚变换有关?
下面还是来具体看一下文章给出的概率模型。首先是问题的形式化,这里要求解的就是两个神经网络的参数,一个生成模板,一个进行配准,用最大后验估计(论文中说的是“似然”,但是我觉得这里应该是最大后验估计/贝叶斯估计)对两个任务进行优化(注意下面的\(\mathcal{V}\)其实就是对应于用来配准的神经网络): \[ \begin{align} \hat{\theta_t}, \hat{\mathcal{V}} & = \arg\max_{\theta_t, \mathcal{V}} \log p_{\theta_t}(\mathcal{V} \vert \mathcal{X}, \mathcal{A}), \newline & = \arg\max_{\theta_t, \mathcal{V}} \log p_{\theta_t}(\mathcal{X} \vert \mathcal{V}; \mathcal{A}) + \log p(\mathcal{V}). \end{align} \] 这里包含两项:似然和先验,其中先验可以用来对形变施加约束,让得到的形变满足一些所希望的性质。
对于先验,作者引入了两点假设:光滑和无偏。记形变场\(\phi_{v_i} = Id + u_{v_i}\),即在恒等变换\(Id\)(identity transformation)上叠加一个残差\(u_{v_i}\),这个残差表示的就是实际的空间偏移(spatial displacement),作者给出的先验是: \[ p(\mathcal{V}) \propto \exp\{-\gamma \Vert \bar{u}_v \Vert^2 \} \prod_{i=1}^{n} \mathcal{N}( u_{v_i}; 0, \Sigma_{u} ), \] 其中\(\bar{u}_v\)是平均偏移\(\frac{1}{n} \sum_{i=1}^{n} u_{v_i} \),这里用的指数函数其实就相当于是假设了\(\mathcal{N}(0, I)\)。先验的第二部分也是用的高斯分布,是每个样例单独的概率,注意这里用了相同的协方差,也即相同的分布,换言之这里认为不同样例的形变场是独立同分布的(独立性让样例的联合概率可以分解成样例各自概率的乘积)。
协方差\(\Sigma_{u}\)省略下标直接记作\(\Sigma\),作者设置其为\(\Sigma^{-1} = L = \lambda_d D - \lambda_a C\),其中\(L\)是(松弛后的)图拉普拉斯矩阵,其对应的是以各个像素为节点所定义的图,\(D\)为度矩阵(degree matrix),\(C\)为邻接矩阵。
先验取对数的结果如下: \[ \log p(\mathcal{V}) = -\gamma \Vert \bar{u}_v \Vert^2 - \sum_{i=1}^n \frac{d}{2} \lambda_d \Vert u_{v_i} \Vert^2 + \sum_{i=1}^n \frac{1}{2} \lambda_a \Vert \nabla u_{v_i} \Vert^2 + \mathrm{const}, \] 其中\(d\)为节点度数,\(\nabla u_{v_i}\)是形变场\(\phi_{v_i}\)也即偏移\(u_{v_i}\)的梯度。注意这里严格来说不应该取等号,另外原文公式(4)符号有点小问题,用的\(u_i\),这里我改成了和原文公式(3)一致的\(u_{v_i}\),不过用哪种都不影响理解。这个式子第一项很直接,第二项也好理解,度矩阵是对角阵,而每个像素的度应该是一样的,所以直接统一乘以度数\(d\)即可,⚡第三项暂时不知道怎么过来的,因为邻接矩阵照理来说是不包含负数的,怎么会计算出梯度来呢?原文这块引用了参考文献17,是作者之前的一个文章,里面确实写了相关的结果,但是也没有推导,结果在引文公式(6)下面,但是那块是直接用的拉普拉斯矩阵得到的结果 [1],而不是邻接矩阵,让人怀疑这两个地方是否矛盾,至少有一个不对?关于多元高斯分布的对数似然,可以参考Wikipedia [2]。
先验的第一项是希望从整个数据集上平均下来看,形变的幅度是比较小的,即学到的模板平均来看和样例都非常接近;第二项和第三项是希望最小化单个样例上形变的幅度和光滑性,⚡这里我感觉很疑惑,为什么要避免光滑?一般情况不都是希望尽量光滑吗?而且论文也说了希望“光滑和无偏”,无偏可以理解,大致对应第一项和第二项,但是光滑这一点上现在反过来了?
对于似然,作者采用高斯分布建模\(\mathcal{N}(x_i; g_{t, \theta_t}(a_i)\circ \phi_{v_i}, \sigma^2 I)\),以变换之后的模板(即对输入的重构)作为均值,加上一个小的噪声作为方差,换言之,将真实的输入看成是重构结果在邻域内进行一个小的扰动所得到的,其实这样建模就相当于是计算均方误差,只不过前面多了一个系数(跟高斯分布的方差有关,方差越小,系数越大,即要求重构误差越小)。关于均方误差和极大似然估计/高斯分布的关系,可以参考这个博文:MSE as Maximum Likelihood。
综合先验和似然,记神经网络的参数为\(\theta = \{\theta_t, \theta_v\} \),对于图像\(x_i\)有: \[ \begin{align} & \mathcal{L}(\theta_t, \theta_v; v_i, x_i, a_i) \newline = & - \log p_{\theta}(v_i, x_i; a_i) \newline = & - \log p_{\theta}(x_i \vert v_i; a_i) - \log p_{\theta}(v_i) \newline = & \frac{1}{2\sigma^2} \Vert x_i - g_{t, \theta_t}(a_i) \circ \phi_{v_i} \Vert^2 + \gamma \Vert \bar{u}_v \Vert^2 + \sum_{i=1}^n \frac{d}{2} \lambda_d \Vert u_{v_i} \Vert^2 - \sum_{i=1}^n \frac{1}{2} \lambda_a \Vert \nabla u_{v_i} \Vert^2 + \mathrm{const} \end{align} \] 原文公式(6)应该是写错了,这里我进行了修改。原文公式(6)第一项明显很奇怪,最小化负的均方误差,相当于在最大化重构的均方误差!?高斯密度函数的指数部分,系数是负的,这里是负对数似然,加了负号,因而要取反变成正的。后面先验的部分照抄了论文前面的公式(4),也没有取反,符号应该也都错了。
通过最小化上面的负对数似然,即可求解所需的参数\(\theta\)。由于模型是用神经网络实现的,因此可以直接用随机梯度下降法来优化。注意到损失函数里面有均值\(\bar{u}_v\)和对样例求和\(\sum_i\),但是如果每次迭代都对所有样例计算一遍,这计算量就非常之大了,原文有提到均值是用了之前\(c\)次迭代的滑动平均来近似(文中取了\(c = 100\)),别的没说,⚡我猜测样例求和那块是不是也是用了类似的做法?还是说就只是针对当前迭代的样例计算?
实验基本都是在MNIST上做的,感觉没啥说服力,不再具体说了。大致结论就是,学到的模板比较清晰(sharp),而不是像直接最小化模板和样例的像素差异那样很模糊,其实这很显然,一个是模板+变换然后重构,一个是直接拿模板来重构,前者当然更好。
在实验设计上其实有些地方还挺好的,分析里面有一个缺失属性和一个隐属性的实验。缺失属性的实验是说在\(a_i\)中去掉某些样例的某些属性,例如去掉数字5的在尺度为0.9到1.1之间的训练样例(其它数字仍然是有这个尺度区间内的样例的),或者完全去掉数字5的训练样例,看还能否生成对应的模板;隐属性的实验是说完全去掉\(a_i\)中的某些属性,例如原来有10维属性,现在去掉数字类别这1维变成9维,看生成的模板能否学到数字类别这一隐属性。缺失属性的实验结果看着还挺好,隐属性的实验结果感觉也还行,给出的例子中,有好几个模板的数字类别是错的,主要是4和9的混淆,还有就是生成的模板和数字差异相对大一些,换言之需要更大幅度的形变才能将图像和模板配准。
分析里面还有一个实验,去掉和加上某个属性,分别学习模板,然后对模板做主成分分析,在两个主成分上变化,以此来生成不同的样例。发现加上某个属性的时候,模板会倾向于学习其它方面的变化,这个还比较符合直觉,毕竟这个属性已经有了输入作为控制了,那模板本身就应该更关注别的变化了,这个还挺有意思的。不过我感觉原文图7中的结果图有可能是挑的,因为两个模型数字选的不一样,不知道实际效果是不是真的如展示的这样明显。
最后有一组实验是在三维脑成像MRI图像上做的,不过感觉主要是给了一些示例结果,要是也能在这上面做一些类似之前MNIST上的那些分析实验就好了,当然,我更感兴趣的其实还是在一般的图像上的结果。除了证明生成的模板在生成效率大幅提高的情况下质量也有所保证,这一组实验主要展示了模型能够按照年龄来生成对应的模板。
这篇文章有一个重要的背景知识:微分同胚变换。关于微分同胚变换,暂时没有去深究,知乎上有人给了从苏大强变换到吴彦祖的图(知乎 - 如何理解微分同胚的概念?),说这就是一个微分同胚变换,虽然感觉很有意思,但是我还是没太具体明白这个变换的特性。。。后面在单独去看看关于这方面的内容吧,毕竟我看这篇文章其实本来就是想看看变换方式的,而目前对于速度场、形变场这些都还没有了解。。。所以说我读文章读着读着就偏了吗 😂

不过目前对从模型设计到实例化(神经网络)这样的写作/研究思路也算是对自己有些帮助吧,自己之前没有特别注意这些方面,缺乏意识。直接描述实例化的模型是比较通俗易懂,不过确实少了一点那种抽象层次的高度,或者说有点思考不够深入的意味。有些约束其实可以直接加,但是这里作者是从后验概率一步步推过来的。看版式这个文章应该是投了NeurIPS,所以至少看上去理论性得稍微强一些才好。
不知不觉竟然精读了这篇文章,花了差不多两天时间,emmm… 😐
[1] \( \Sigma_z^{-1} = \Lambda_z = \lambda L \),\( \mu^{\mathrm{T}} \Lambda_z \mu = \frac{\lambda}{2} \sum_i \sum_{j\in N(i)} (\mu[i] - \mu[j])^2 \),其中\(L\)是拉普拉斯矩阵,\(N(i)\)表示体素\(i\)(voxel)的邻居集合(这篇文章考虑到而是三维校准,所以是体素不是像素)。这里我对原文公式按照自己的理解做了修改,外层求和增加下标\(i\),内层求和\(N(I)\)改成\(N(i)\),这样公式更加清晰好懂,另外在不影响理解的情况下,我去掉了\(\mu\)的下标。
[2] 多元高斯分布的对数似然:\( \ln L = -\frac{1}{2} [ \ln \vert \Sigma \vert + (x - \mu)^{\mathrm{T}} \Sigma^{-1} (x - \mu) + k \ln 2\pi ] \)